導(dǎo)讀：射頻技術(shù)服務(wù)于現(xiàn)代通信與電子戰(zhàn)，但是射頻只是一個(gè)載體，真正有用的“信息”是基帶信號(hào)，信號(hào)的傳輸類型對(duì)整個(gè)射頻方案的設(shè)計(jì)起著決定性的作用。

在設(shè)計(jì)射頻方案時(shí)，射頻工程師都會(huì)發(fā)出靈魂一問“恒包絡(luò)還是非恒包絡(luò)？非恒包絡(luò)峰均比幾？”

今天就來說一下這些恒包絡(luò)調(diào)制和非恒包絡(luò)調(diào)制。

一、恒包絡(luò)

設(shè)一個(gè)符號(hào)為g(t)*cos(ω₀t+φ)，g(t)為矩形開關(guān)選通脈沖[頻域?yàn)镚(jω)]，非線性用3次函數(shù)逼近Vo=aVi+bVi2+cVi3，則

Vo=a* g(t)*cos(ω₀t+φ)+b* g2(t) *cos²(ω₀t+φ)+c*g3(t) *cos³(ω₀t+φ);

cos³(ω₀t+φ)=cos(ω₀t+φ)*cos²(ω₀t+φ)=1/2*cos(ω₀t+φ)*[cos(2ω₀t+2φ)+1]

=1/4*cos(3ω₀t+3φ)+3/4*cos(ω₀t+φ)

Vo=a*g(t)*cos(ω₀t+φ)+b* g²(t) *cos²(ω₀t+φ)+c/4*g³(t)* cos(3ω₀t+3φ)+3c/4*g³(t)* cos(ω₀t+φ)

輸出的基頻為Vo=(a+3c/4)* g(t)*cos(ω₀t+φ)

∵g³(t) =g(t)

所以恒包絡(luò)基本上沒有三階互調(diào)問題。

但矩形脈沖g(t)的頻譜（sinc函數(shù)）副瓣太高，會(huì)泄漏到鄰道。

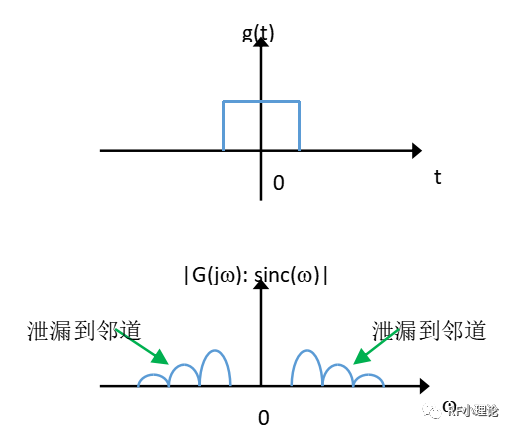
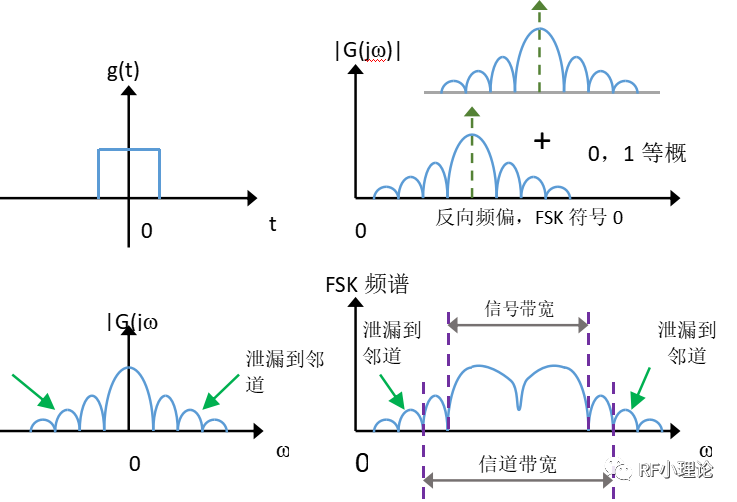
從時(shí)域上來看，幅度不變化的，就是恒包絡(luò)調(diào)制。所以FSK，GMSK,MSK，OQPSK都是恒包絡(luò)調(diào)制。

這里要特別說一下QPSK，從星座圖上來看，QPSK的幅度都是相同的，但是為什么QPSK不是恒包絡(luò)？

從立體圖上看，QPSK是一個(gè)調(diào)幅調(diào)相的信號(hào)，雖然幅度都是恒定的，但是相位有變化00,01，10,11，從01到10需要經(jīng)過零點(diǎn)，經(jīng)過原點(diǎn)的某瞬及幅度就為0了（實(shí)際上是非常小），這樣的話整個(gè)信號(hào)峰均比就會(huì)變大，所以QPSK是非恒包絡(luò)。

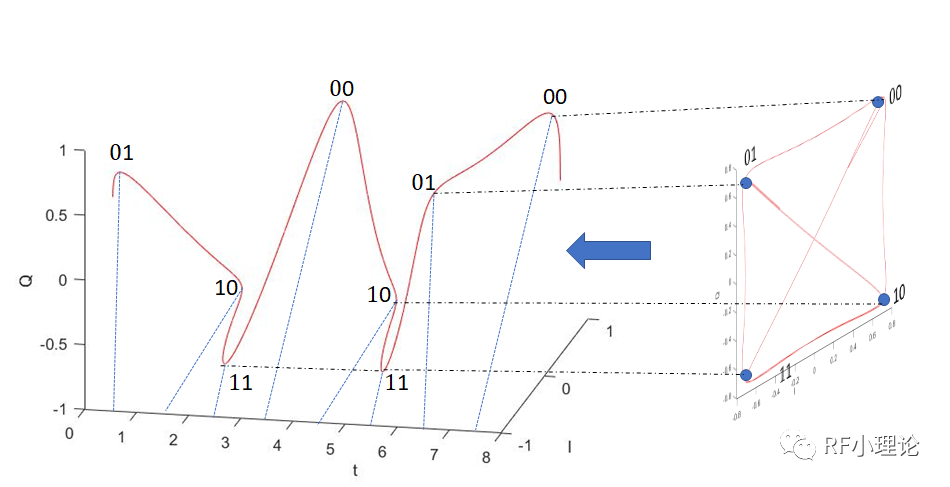
二、非恒包絡(luò)

設(shè)一個(gè)符號(hào)為g(t)*cos(ω₀t+φ)，g(t)為滾降包絡(luò)開關(guān)脈沖，由于非線性，用3次函數(shù)逼近Vo=aVi+bVi2+cVi3，則

Vo=a* g(t)*cos(ω₀t+φ)+b* g2(t) *cos2(ω₀t+φ)+c*g3(t) *cos3(ω₀t+φ);

Vo=a*g(t)*cos(ω₀t+φ)+b* g2(t) *cos2(ω₀t+φ)+c/4*g3(t)*cos(3ω₀t+3φ) +3c/4*g3(t)* cos(ω₀t+φ)

輸出的基頻為Vo= [a*g(t)+3c/4*g3(t)]*cos(ωt+φ)

x(t)*y(t)←→1/(2π)*X(jω)?Y(jω)，f(t)?d(t)=f(t)

cos(ω0t+φ) ←→π[d(ω-ω0) *ejφ+d(ω+ω0) *e-jφ] ，

3c/4g3(t)*cos(ω₀t+φ)←→3c/8*ejφ*G3(jω-ω0)+3c/8*e-jφ*G3(jω+ω)

非線性增加了一項(xiàng)基頻3c/4g3(t)*cos(ω₀t+φ) ，但有別于信號(hào)頻譜，包絡(luò)不同。

滾降包絡(luò)因子g3(t)的頻譜;

g3(t)= g(t)* g(t)* g(t)

g3(t) ←→1/(2π)*G(jω)*[1/(2π) G(jω)*G(jω)]

還是以QPSK為例，可以看到QPSK的幅度在變化。

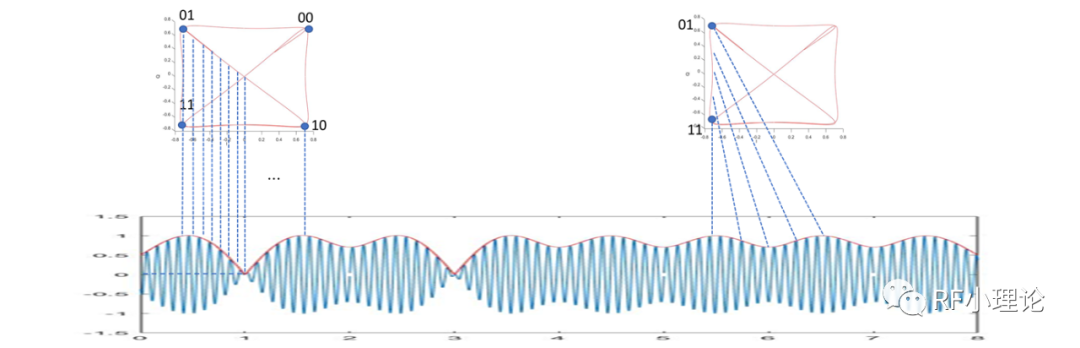
講了這么多，問題的關(guān)鍵是：射頻工程師為什么要分析調(diào)制包絡(luò)？？

因?yàn)樵趯?shí)際中，我們經(jīng)過了調(diào)制之后的信號(hào)，因?yàn)楸容^微弱，還需要經(jīng)過功放（功率放大器）的放大才發(fā)射出去。

恒包絡(luò)調(diào)制因?yàn)樾盘?hào)幅度完全相同，不會(huì)產(chǎn)生三階互調(diào)，所以對(duì)射頻的設(shè)計(jì)沒有線性要求，方案設(shè)計(jì)上簡(jiǎn)單很多。

非恒包絡(luò)調(diào)制為了使得信號(hào)在經(jīng)過放大之后不失真，我們需要使用線性功放。但是線性并不能無限回退，我們需要在以[敏感詞]成本、[敏感詞]功耗設(shè)計(jì)指標(biāo)。所以根據(jù)包絡(luò)信號(hào)的峰均比、EVM我們可以選擇合適的線性器件。

結(jié)語：射頻設(shè)計(jì)的最重要思想就是線性，而制約線性設(shè)計(jì)的最重要因素就是信號(hào)的包絡(luò)方式，雖然調(diào)制方式不歸射頻工程師，但是對(duì)常見的調(diào)制方式的優(yōu)劣勢(shì)有所了解，對(duì)成為一個(gè)系統(tǒng)工程師還是有一些幫助的。





免責(zé)聲明：本文采摘自網(wǎng)絡(luò)RF小理論，本文僅代表作者個(gè)人觀點(diǎn)，不代表金航標(biāo)及行業(yè)觀點(diǎn)，只為轉(zhuǎn)載與分享，支持保護(hù)知識(shí)產(chǎn)權(quán)，轉(zhuǎn)載請(qǐng)注明原出處及作者，如有侵權(quán)請(qǐng)聯(lián)系我們刪除。